This section records how the authors’ new equation for calculating osmotic potential was modified and used to estimate the osmotic potentials of both inorganic and organic water (aqueous) solutions over a wide temperature range with low to high solute concentrations under normal atmospheric conditions.
The formulation of the equation.
The authors’ “new equation” to equate the pressure across a semi-permeable membrane that separates pure water from a water solution as:
Po = P1 – Px + Py + Ph (1)
In which:
Po = osmotic or external pressure. The osmotic potential is the negative value of Po.
P1 = pressure exerted by the solute free or “pure” water separated by a semi-permeable membrane from a water solution.
Px = pressure exerted by the “free” water in the solution; that water not attached to solute particles, and in the theoretical absence of solutes. This is the result of increasing the average distance traveled by the water molecules during the “cooperative structural relaxation” phase of liquid water as discussed by Stillinger and Rahman (1972) and Sarkisov et al. (1974). -An individual molecule is visualized as an integral part of an intermittent tetrahedron structure; for a fraction of time it is free to move.
Py = pressure lost by the free water to keep the solute particles in solution.
Ph = pressure lost by the free water to keep the water firmly held or “bound” to the solute particles in solution.
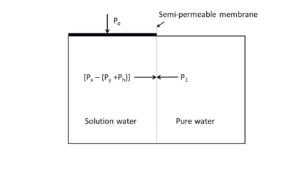
Figure 1. An illustration of the pressures between an aqueous solution and pure water across a semi-permeable membrane divide, as formulated by Equation 1.
In Equation (1) it may be noted that “P1 – Px” is the pressure difference between the potential of pure water and the solution water in the theoretical absence of solutes. In the solution state, the solute particles are considered to be a spacing mechanism. By increasing the space between the water molecules, the distance they travel during the cooperative structural relaxation phenomenon is increased. Conversely, the force of collision with one another is decreased by the square of the time taken for the extra distance they travel; this results in a considerable loss of force. In the case of the solute molecules, the energy for their maintenance in the solution state is drawn from the free water molecules, and taken into account by pressure Py. Pressure Ph takes to account the loss of energy of the free water molecules to keep water molecules firmly held to solute particles, in solution.
Eq.(1) was revised as detailed by Cochrane and Cochrane (2007), as:
Po = {m/2 Nw2/3 [(V/Nw)1/3 – 2erw] /(At2)} –
{m/2 Nf2/3 [(V/Nw)1/3 – 2erw]2/(At2)/[(V/Nf)1/3 – 2erw]} +
{m/2 Np2/3 [(V/Nw)1/3 – 2erw]2/(At2)/[(V/Np)1/3 – 2erp]} +
{m/2 Np Nh [(V/Nw)1/3 – 2erw] /(At2Nw1/3)} (2)
The symbols used in Eq.(2). and their definitions are summarized in Table 1.
Table 1. Symbols, definitions, and values for the osmotic potential equation.
| Symbol | Definition and values used |
| A | Unit area of the semipermeable membrane surface (m-3) |
| m | Mass of a molecule of water (kg). “m” was calculated as 2.9915073 x 10-26kg. ([mol. wt. of H2O] / [Avogadro’s number] / 103). Note: Avogadro’s number = 6.0221415×1023; mol. wt. of H2O = 18.01528. |
| Nw | Number of water molecules per unit volume V in pure water. Nw was calculated as 3.3368797 x 1028. ([ Sp.Gr. of water at 200C] / m x 103). Note: the Sp.Gr. of water at 200C = 0.99823. |
| V | Unit volume (1 m3) |
| erw | Effective average radius of a water molecule that reduces the distance traveled during cooperative structural relaxation (m). The value was calculated using the spherical rotational envelope of a static water molecule given as 22.5 cm3 mol-1 suggested by Conway (1981). This was calculated as 3.607 x 10-12m, by the expression:
((1/ Nw)1/3 – (((1 – ((22.5/[Avogadro’s No.]/18.01528)Nw)) / Nw)1/3))/2. |
| t | Average time taken for a water molecule in pure water to travel during structural relaxation phase of pure water. It was calculated as 2.05 x 10-12s on the basis of calculations giving the best fit at the temperature of 200C10 . |
| Nf | Number of “free” water molecules per unit volume V, of solution. Nf was calculated for solutions at 200C as: ([(a – b)/g] – (d x b / c x e x Nh)) x 106
in which: a = relative density of solution at 200 C, kg dm-3 b = anhydrous solute concentration, kg x 10-3 dm-3. c = molecular weight of solute. d = number of ions the compound gives on solution. e = Avogadro’s number (6.0221415 x 1023 was used) g = mass of one water molecule (2.9915073 x 10-26 kg). Note: ‘a’ and ‘b’ were taken from the tables of “Concentrative Properties of Aqueous Solutions” recorded in Weast (1983). |
| Nh | Mean number of water molecules firmly held or “bound” to the particles in solution; i.e. the inner hydration sphere. The values used in the calculations fall within the ranges given by various authors including Conway (1981). |
| Np | Number of solute particles (molecules and, or ions) per unit volume V, of solution. Np was calculated as: [d x b / c x e]. ‘d, b, c and e’ have been defined for the calculation of Nf, above. |
| erp | Effective mean radius of the rotational envelope of solute particles with or without held water molecules (m) as the case may be, that reduces the distance traveled by solute particles during the cooperative structural relaxation of the free solution water. It was estimated on the basis of best statistical fit, in the absence of any reliable recorded information by Cochrane and Cochrane (2007).. |
Adjustments to the “new equation” to estimate osmotic potentials at different temperatures.
It was considered that Eq. (2) could be used to calculate the osmotic potentials of inorganic and organic aqueous solutions at different temperatures by adjusting three of its factors for any desired temperature, viz: 1) The volume property of the pure water, 2) “Nf” the number of “free” water molecules per unit volume (V) of solution, and 3) The “t” factor expressing the cooperative structural relaxation time of the solution water. These factors are discussed as follows:
1) Volume properties of water at 1 atm over the range of 0 to 1000C are recorded by Weast (1983) in terms of kg m-3.
2) Relative density data for solutions is recorded for a temperature of 200C by Weast (1983), however, very little data was found in the literature for other temperatures. Consequently, in order to estimate “Nf” the number of free water molecules per unit volume (V) of a solution, equations were provisionally formulated to provide approximate estimates at a given temperature. For organic solutions a proxy equation was formulated as:
Nf(organic)=([1000-((M∙Mw)/RD)]∙Mw+M∙Mw)/1000 (3)
In which:
M = molar concentration of the solution
Mw = molecular weight of water
RD = relative density of solute (gcm-3)
Eq. (3) was modified for inorganic solutions as:
N f(organic)=([1000-((M∙Mw)/(RD∙(1/1.33) ))]∙Mw+M∙Mw)/1000 (4)
In which:
The factor “1/1.33” is a fitted value added to Eq.(3) to very approximately compensate the effect of water strongly held to solution solutes.
Equations (3) and (4), which are clearly approximations, were nevertheless tested at 200C over a series of solutions with wide ranges of solute concentrations, and the calculations compared with “Nf” calculations using the equation recorded in Table 1 with measured relative densities of solutions15; Eq. (3) for sucrose, D- glucose, glycerol, maltose, lactic acid, D-mannitol, urea, and Eq. (4) for NaCl, NH4Cl, CaCl2, KCl, KI, MgSO4, and NaNO3. The “Nf” values of the latter were substituted into the equation for calculating “Nf” using measured relative densities recorded in Table 1, and the relative densities of their solutions calculated. As shown in Tables 2 and 3, those latter values compared well with the recorded relative density values. –Consequently, due to the lack of relative density information for temperatures of solutions above 200C, Eqs.(2) and (3) were used to provide tentative, approximate estimates.
Previous work by the authors (2007) had estimated the “t” value, the average time taken for a water molecule in pure water to travel during the “cooperative structural relaxation phase”, as 2.05-12 s for a temperature of 200C. This had been established by comparing the osmotic pressure calculated with the new equation with that of recorded data over wide concentration ranges of both NaCl and sucrose solutions.
To estimate the values of “t” over a wider range of temperature, the “Nf” values estimated for NaCl and sucrose at 200C by Eqns.(3) and (4) were first substituted into Eq.(2) to compare their calculated osmotic potentials at the “t” value of 2.05-12s with those established by past work (Cochrane and Cochrane 2007) it was found that the R2 of the comparisons of their osmotic potential values were highly significant. In view of this finding, in order to establish provisional osmotic potential values over a wider temperature range, it was decided to substitute the “Nf” values as calculated at a given temperatures for the NaCl and sucrose solutions via Eqs.(3) and (4) into Eq. (2), together with values of “t” corresponding to those temperatures as recorded in the literature. The “t” values estimated by Davis and Jarzynsky (1972) from Raman spectrum data by Wairafen (1968) over the 0 to 400C range were first used as they calculated the “t” value at 200C as 2.05-12s, the same value as calculated by the authors. However, as noted by Endo (1979), “t” values calculated at different temperatures vary between authors, calculation methods and the different experimental methodology. To illustrate how different “t” values would affect the estimation of osmotic potentials of solutions over wide concentration levels of organic and inorganic solutes, the “t” values re-calculated by Endo (1979) on the basis of values calculated by Davis and Litovitz (1965) were subsequently compared with those of Davis and Jarzynski (1972), from 0 to 400C to go a little above the normal human body temperature of approximately 370C.